PLL 中的 DSM 可以用全数字的方法实现，因此可以用 Simulink 工具建模，进行功能仿真和功率谱仿真，再用 Verilog 实现。

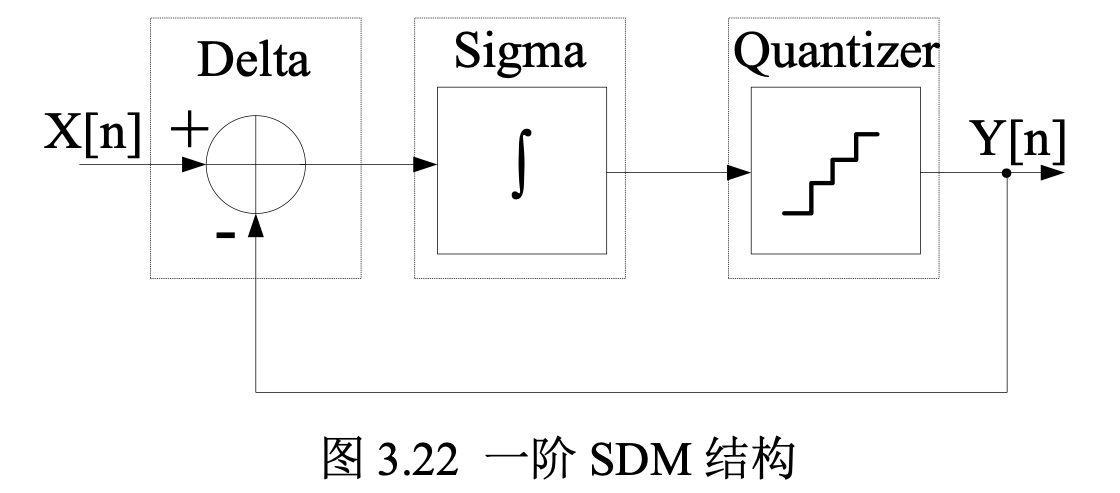
一阶 DSM 传递函数计算

如上图所示，一阶 DSM 由一个 Delta 调制器，一个积分器以及一个量化器组成。

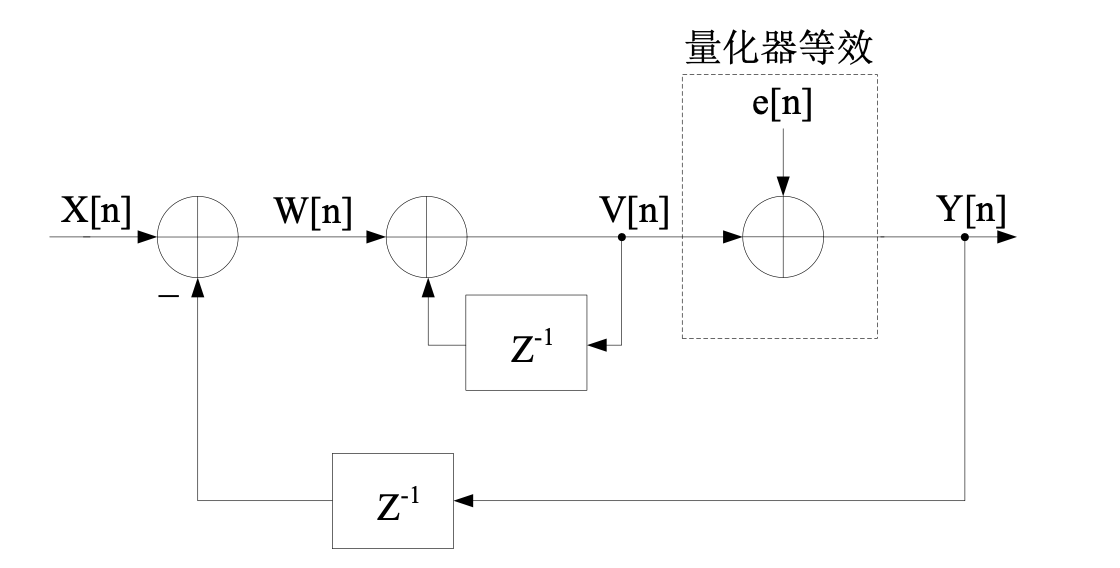
image-20201127221245628

一阶 DSM 等效的 Z 域模型如上图所示，其中量化器等效为一个噪声的叠加，可以得到： $W [z] = X [z] - z^{- 1} Y [z] V [z] = W [z] + z^{- 1} V [z] Y [z] = E [z] + V [z]$ 可以推导出传递函数为： $H [z] = \frac{1}{1 - z^{- 1}} Y [z] = X [z] + (1 - z^{- 1}) E [z]$ 以及： $S T F = \frac{Y [z]}{X [z]} = \frac{H [z]}{1 - z^{- 1} H [z]} = 1 N F T = \frac{Y [z]}{E [z]} = \frac{1}{1 + z^{- 1} H [z]} = 1 - z^{- 1}$ 可以看到，一阶 DSM 对输入信号起到传递作用，增益为 1，而对噪声起到了高通滤波作用，因此实现了对噪声的整形，将噪声推向高频。

由上式还可以推出： $V [z] = X [z] + (V [z] - Y [z]) z^{- 1}$ 由此可以得到该 DSM 的另一种 Z 域模型：

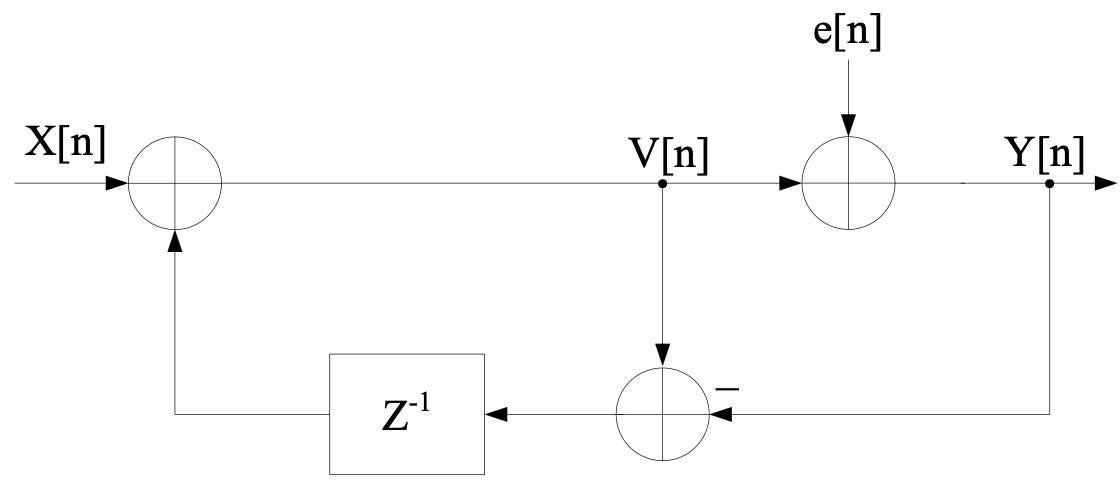
image-20201127223250969

可以看到该一阶 DSM 本质上就是一个累加器，因此其在电路中信号流图可以描述如下：

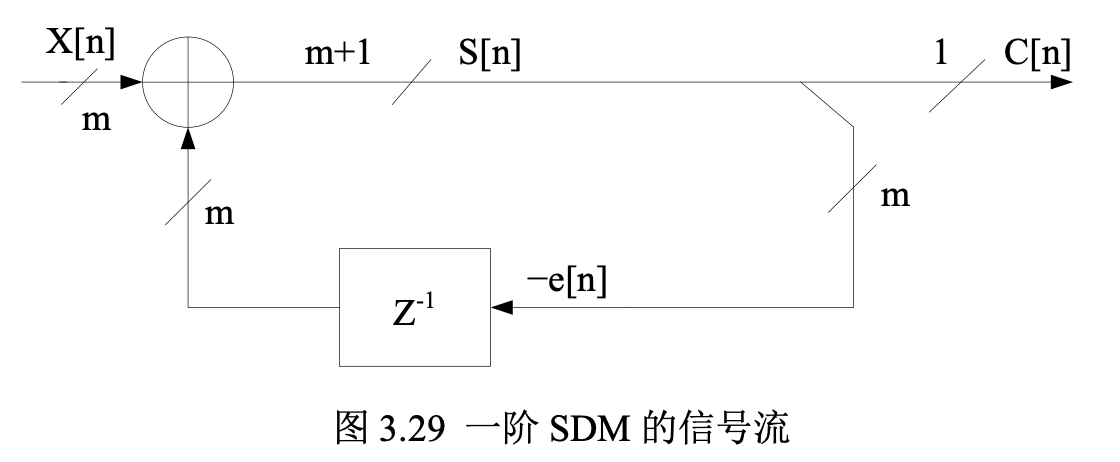
image-20201127223534482

其中累加器为两个 m 位输入，m+1 位输出，输入 $X [n]$ 为缩放到 $2^{m}$ 的小数部分，例如，当 m = 24 时， $X [n] = 6291456$ 表示输入为 0.375 ( $6291456 / 2^{24} = 0.375$ )。 $C [n]$ 为累加器输出结果的最高位，是累加的进位，相当于量化器的量化输出结果。累加器输出的低 m 位相当于量化误差。上面的结构可以用如下电路来实现：

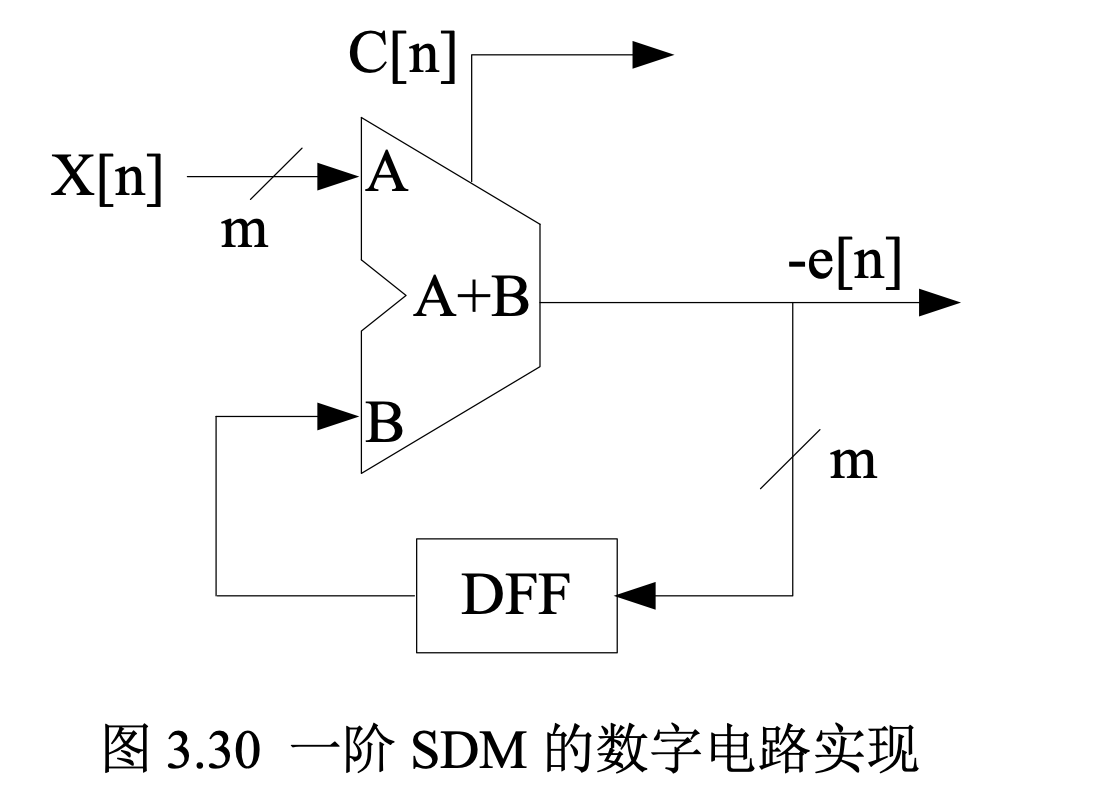
image-20201127224405414

其中 DFF 为 D 触发器，实现了延迟的功能。

一阶 DSM Simulink 仿真

根据上面的分析，可以在 Simulink 中对一阶 DSM 进行仿真。Simulink 中的结构如下图所示：

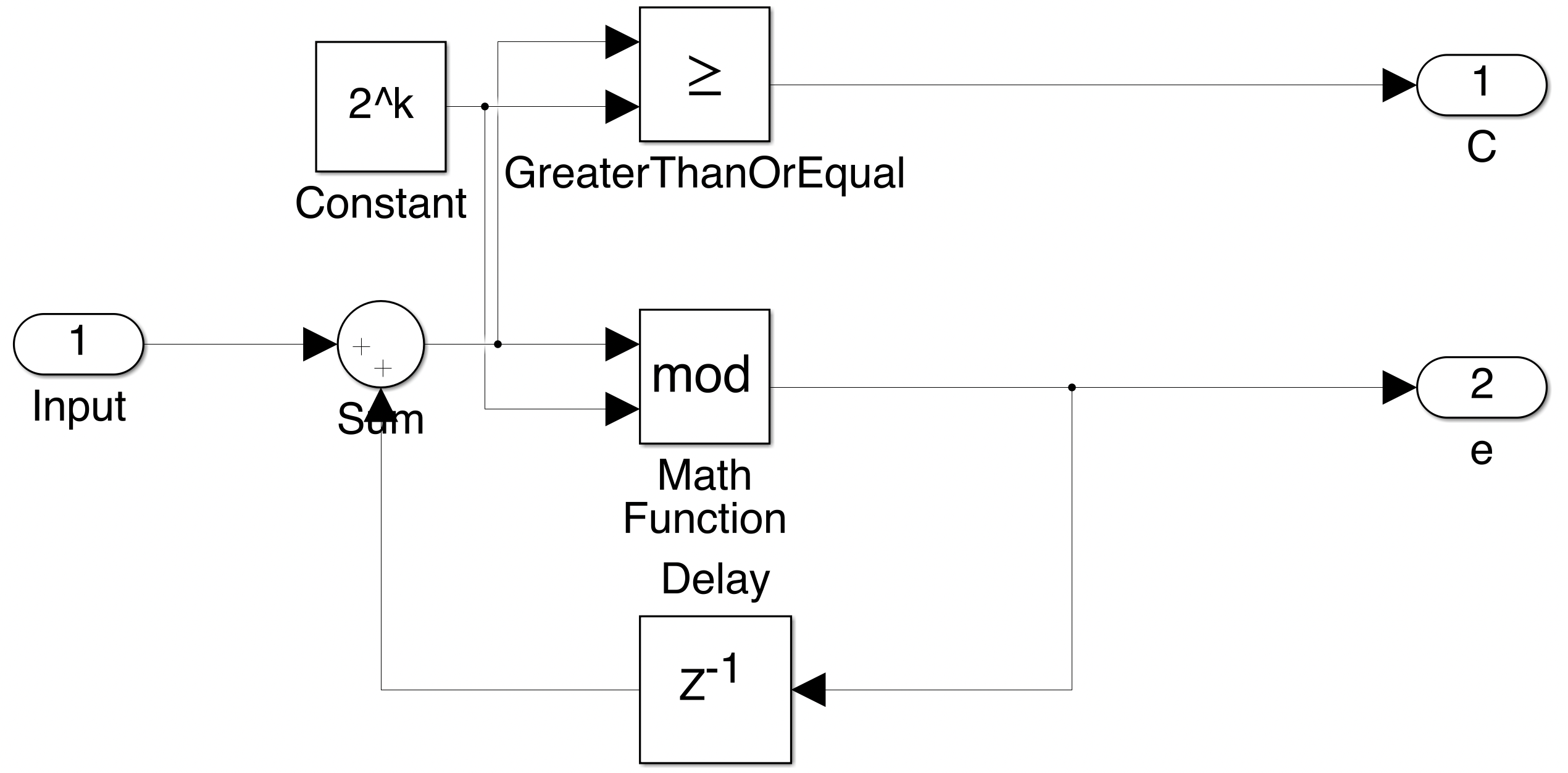
截屏2020-11-27 下午10.48.32

累加器进位使用一个大于等于的比较运算实现，累加器的低位输出使用取余运算实现。

OneStage

一阶 DSM 仿真结果如上图所示，第一个图是量化输出 C，第二个图是误差输出 e，输入设置为 6291456，累加器设置为 24 位，可以看到量化输出 C 每 8 个周期中会有 3 个高电平。

MASH1-1-1

一阶的 DSM 输出周期性很明显，对噪声的整形效果不好。可以将其级联起来组成 MASH1-1-1 结构，如下图所示：

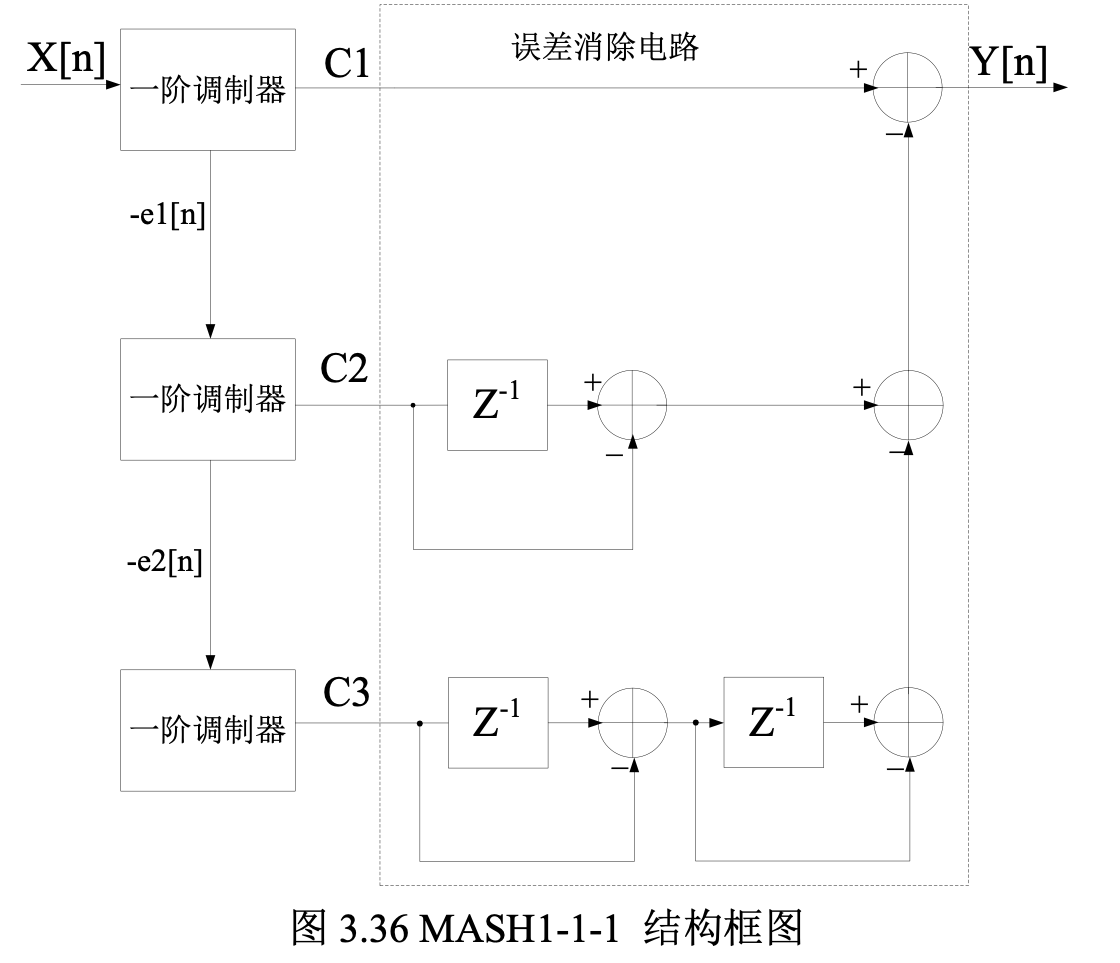
image-20201127225717497

前一级的一阶 DSM 误差作为下一级的一阶 DSM 输入，每一级的输出通过延迟相加得到最终输出，传递函数推导如下： $C_{1} = e_{1} [n] * (1 - z^{- 1}) + X [n] C_{2} = e_{2} [n] * (1 - z^{- 1}) - e_{1} [n] C_{3} = e_{3} [n] * (1 - z^{- 1}) - e_{2} [n] Y [n] = C_{1} + C_{2} (1 - z^{- 1}) + C_{3} (1 - z^{- 1})^{2}$ 可以得到： $Y [n] = X [n] + e_{3} [n] * (1 - z^{- 1})^{3}$ 可以看到最终输出的噪声只和第三级的噪声有关，并且对第三级噪声做了高阶整形。

MASH1-1-1 Simulink 仿真

Simulink 中的结构如下图所示：

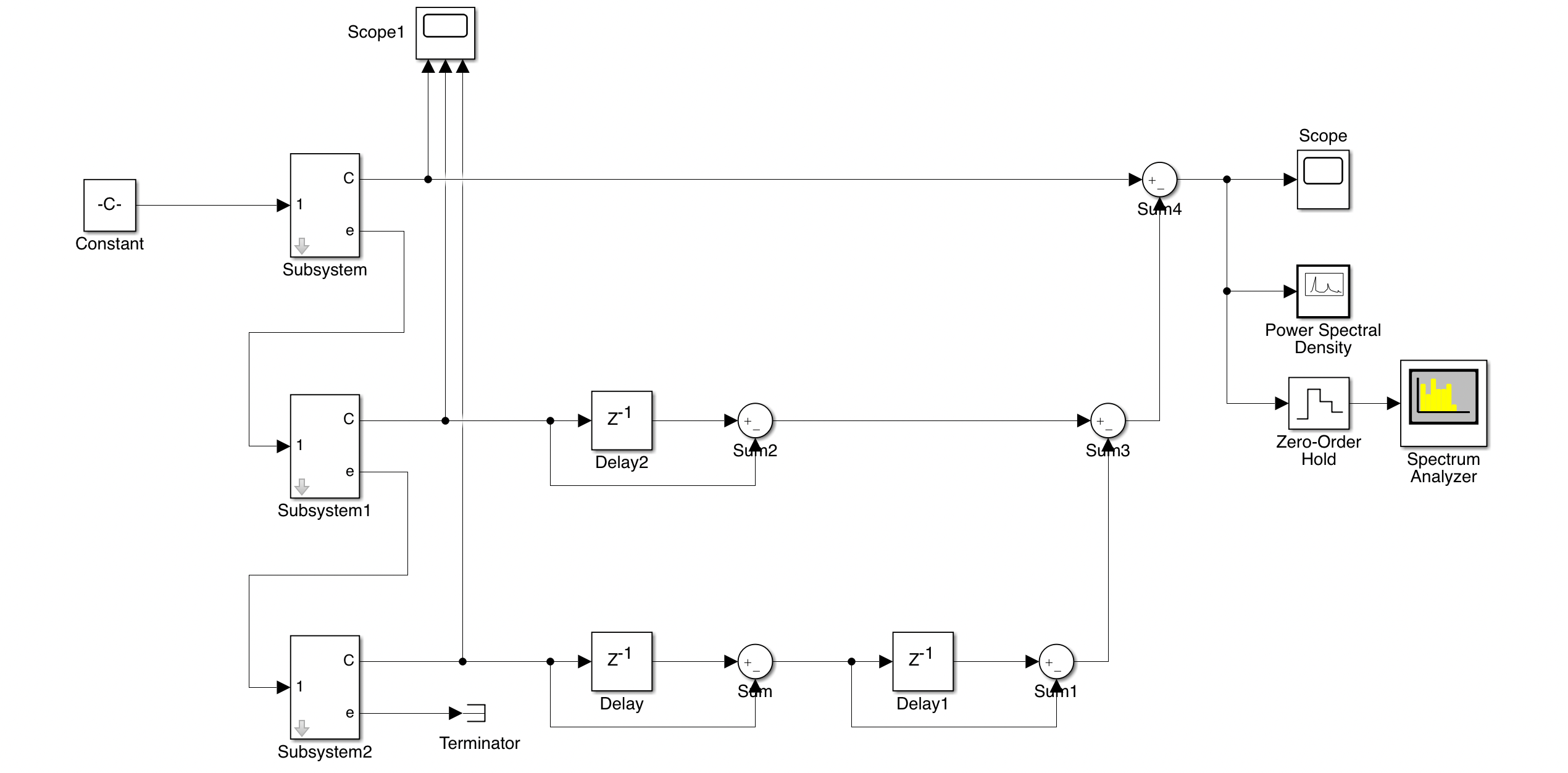
截屏2020-11-28 上午9.14.25

当输入为 0.375 ( $6291456 / 2^{24} = 0.375$ )，输出如下：

ThreeStage6291456

当输入为 0.1 ( $1677721 / 2^{24} = 0.1$ )，输出如下：

ThreeStage1677721

当输入为 0.9 ( $15099494 / 2^{24} = 0.9$ )，输出如下：

ThreeStage15099494

输出信号的功率谱密度：

PSD

结果分析：

从上面仿真的结果可以看到 MASH1-1-1 结构的 DSM 可以实现对噪声的高阶整形，将噪声推向高频。

MASH1-1-1 结构的 DSM 理论上输出范围是 [-3,4]，但实际上输入不同的值，输出范围也是不同的，某些输入值对应的输出周期性还是比较明显的，例如输入为 0.375 的时候。看论文上说要在低位加 dither，可以改善这种情况，让输出的随机性更高。

参考文献

[1]Y. Wu, M. Shahmohammadi, Y. Chen, P. Lu and R. B. Staszewski, "A 3.5–6.8-GHz Wide-Bandwidth DTC-Assisted Fractional-N All-Digital PLL With a MASH $$ -TDC for Low In-Band Phase Noise," in IEEE Journal of Solid-State Circuits, vol. 52, no. 7, pp. 1885-1903, July 2017, doi: 10.1109/JSSC.2017.2682841.

[2]周晖. 小数N频率综合器中Sigma-Delta调制器的研究与设计[D].西安电子科技大学,2014.